|

Carta #29 - 2010
Tema: Area cuadrada de coronación
Fecha: 08/01/10 11:21:00 PM EDT
De: Salem22
Para:
service@chess-poster.com
Hola,
Encuentro el portal de ustedes como algo muy vasto y completo a tal punto que lo considero como mi "Enciclopedia de Ajedrez en
linea" para todas mis presentes y futuras referencias.
Aún así, no he podido encontrar ninguna información en su página en relación con una maniobra de Ajedrez poco conocida y que es llamada 'Area cuadrada de Coronación'. Esto se refiere a el area cuadrada mínima que se requiere para que un Peón pueda promoverse a Reina.
Esto aplica solamente a finales de Rey y Peón, por supuesto.
Gracias.
Estimado visitante,
El area cuadrada de coronación es un método simple para encontrar si un Peón puede estar posibilitado a coronarse en un final de Rey y Peón calculando si el Rey oponente puede capturar a un Peón antes de alcanzar la octava hilera.
Consideremos la siguiente posición: la fig. 1 muestra a un Peón en la casilla b4 con la posibilidad de coronar en cuatro movimientos:
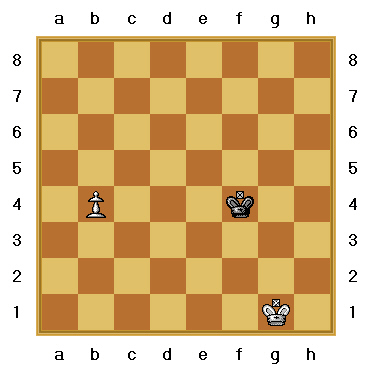
Fig. 1
Ahora, dibujemos una area cuadrada imaginaria (fig. 2) a partir de la posición actual del Peón hasta la casilla de coronación de b8 o diagonalmente a la casilla f8, en este caso una area cuadrada de 5x5 casillas. Sí el Peón blanco y el Rey enemigo están
dentro de esta area, entonces el Rey negro podrá detener el avance del Peón blanco antes de promover, sin importar quién mueve a continuación.
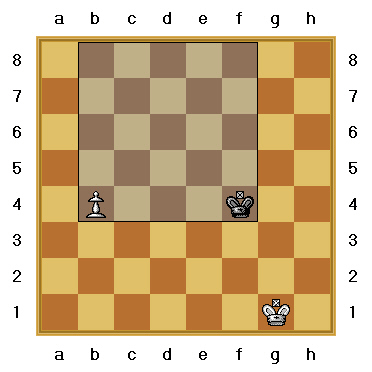
Fig. 2
En esta posición un poco diferente (fig. 3), el Rey negro en la casilla g3 está colocado fuera del area cuadrada de coronación. Sí el Peón blanco mueve primero, puede promover a Reina ya que cada vez que que el Peón se desplaza hacia adelante una casilla, el area cuadrada de coronación se reduce (a 4x4) y el Rey negro nunca podrá posicionarse dentro de esta area.
Por otro lado, sí el Rey negro mueve primero, puede entrar dentro del area cuadrada de coronación y así detener el avance del Peón blanco.
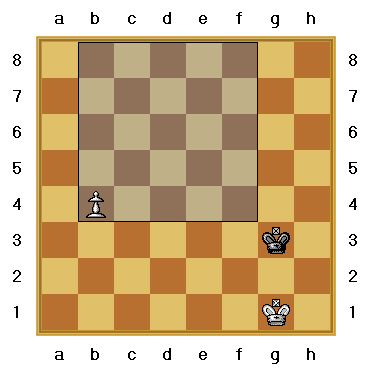
Fig. 3
Gracias por visitarnos,
chess-poster.com |